为什么java在hashmap中使用红黑树?

为什么`Java8`在`HashMap`中使用红黑树?

众所周知, Java8在HashMap结构的实现中, 做了一个重大改进,引入了红黑树. 红黑树俨然已经成为一个大热门, 经常听闻有人要在面试中手写一个正确的红黑树实现之类的流言. 红黑树科普资料已经汗牛充栋.

不过这里,我们不考虑2-3树,2-3-4树,红黑树,左倾红黑树之类的实现, 主要是看一看,探寻下:为什么当初会选择引入红黑树, 究竟遇到了什么问题,解决了什么问题.别的语言有没有遇到这个问题,是怎么解决的.

JEP

Java语言如果有什么大的改动, 都是先由JEP(java enhance proposal) 开始.目前可以查到, 在JEP180 (JEP 180: Handle Frequent HashMap Collisions with Balanced Trees)中, 是关于这部分代码的讨论.这里说, 要用平衡树来解决频繁碰撞问题.

所以, 问题变成了3个.

频繁碰撞到底是什么?
Java 为什么要用平衡树?
平衡树里为什么要选红黑树?

频繁碰撞可能吗?

哈希表(Hash Table), 俗称关联数组( associative array ) . 使用一个哈希函数 (Hash Function) 来计算key在数组中的索引(Index)位置. 理想情况下, 每一个key都会被计算到一个唯一的位置. 然而, 现实中因为各种原因, 会对多个不同的key计算出同一个数组位置(这个位置可以称为slot或者bucket). 这种现象叫哈希碰撞(hash collisions).

先做个简单的数学题

假设我们有M个抽屉,N个小球, 现在随机把小球放到抽屉里,所有小球都在同一个抽屉的概率有多大?

根据中学知识可以知道, N个球,每个球都有B种选择可能性,完全随机放可以产生的结果有$M^N$种结果.所有球都放进同一个抽屉, 只有M种可能. 计算概率应该为 $\frac{M}{M^N}=(\frac{1}{M})^{N-1} $.

同理,对于Bucket数为b的哈希表,理想情况下,出现n个key被哈希函数计算到同一个位置的概率为$(\frac{1}{b})^{n-1}$.

java.util.HashMap的旧版本的实现里, 用的拉链法(数组+链表).

初始数组长度 (DEFAULT_INITIAL_CAPACITY)=16.
默认负载因子(DEFAULT_LOAD_FACTOR)=0.75
容量超出了 16 * 0.75=12个, 那么会发生扩容.

在发生扩容之前, 所有key全被hash计算同一个slot的概率是多大?

当 n=12时, ${¹⁄₁₆}^{11}=0.0000000000009094947017729282379150390625$

对 n=8时$(¹⁄₁₆)^7=0.0000000037252902984619140625$

这个8就是HashMap发生树化的阈值TREEIFY_THRESHOLD

所以, Java8就为了这亿分0.3概率发生的事情,改了代码?难道是为了将来故意为难面试者?即使哈希函数实现的再差,也不会有这种情况发生吧.

道高一尺魔高一丈

哈希表到底要设计的多复杂,往往不是取决于防守者,而是来自攻击者.一般情况下不会发生, 二般情况下,往往就发生了.

2003年有一篇神奇的文章基于算法复杂度的DOS攻击(Denial of Service via Algorithmic Complexity Attacks). 这篇文章里,就提出了攻击的方式,利用人为的key选择,针对hash函数的均匀性进行攻击.让所有的节点都落到相同的slot里.让哈希表在最差的情况下,退化成一个链表.

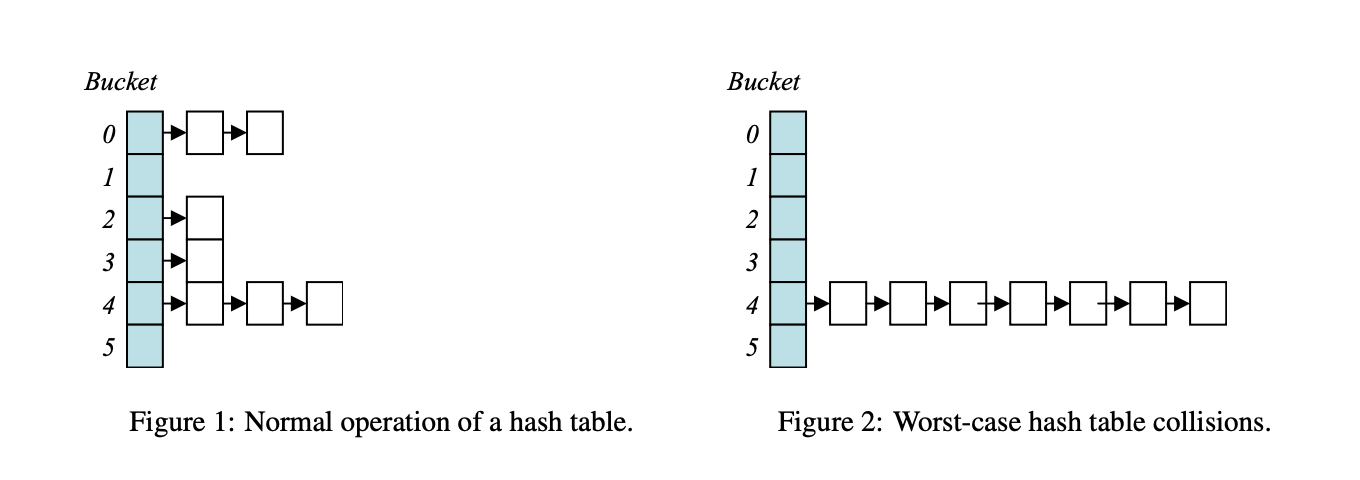
一个简单的小例子, 先取一个最简单的哈希函数算法, 比如对输入数字求和,最终结果模10,获得一个10以内的数字.别笑, 这个虽然简单,但是这真的是一个算法Luhn algorithm.对这个算法, 通过增加N对相加为10的数, 就可以得到N多校验和是同一个数的内容.

这个攻击, 主要特点, 就是操纵数据, 来攻击哈希函数. 能否成功取决于3点:

哈希函数结果是可预测的
最坏场景(worst-case)性能糟糕
输入key个数上限比较高

治疗方案

针对这几个点, 解决方案也是几大类.

数据控制
哈希表和完美哈希

平衡树

graph TD
	解决问题 --> 解决数据输入 --> 限制参数长度
解决问题     --> 解决哈希函数 --> 哈希带随机种子
	解决哈希函数  --> 全域哈希
	解决问题 -->解决最坏场景  --> 平衡树方案

在刚出现这个攻击方式的时候, 一般是走的第一条路, 对数据长度进行限制.

在Java8 采用JEP180之前, 其实尝试过第二条路. 给String添加一个私有的属性hash32,新的hash算法,murmur3 hashing algorithm along with random hash seeds and index masks.

然而, 这个方案有几个额外问题.

修改了原string接口
不能适用用非string做key的场景
造成了某些回归测试无法通过
增加属性会占用堆空间.

东风来了

在HashMap正在紧锣密鼓增加hash32的时候, 东风来了.ConcurrentHashMap在Java8中的JEP155改造成功了, 率先实现了平衡树. Java坚持了他的保守性, 在对String类的修改未暴露到社区之前,移植了平衡树的实现回来, 按照第三个方案实现了攻击防御.

最后一个问题

前2个问题都找到了答案.第三个问题,变成了.

`ConcurrentHashMap` 为什么会在`平衡树`里选择`红黑树`?

JEP 155的核心点, 就是一句话cache-oriented enhancements.

平衡树有很多种,单单文章提到的,就有

red-black tree
splay tree
treap
avl
B-tree
2-3 tree

这里面

2-3树其实就是一种特化的B-树
红黑树是2-3树的一个特化.
树堆的最坏场景是$O(n)$,解决不了问题.
伸展树在最坏场景下也不是很合适.

真正能够值得一比较的, 只有 AVL和红黑树.

Algorithm	Average	Worst case
Space	$O(n)$	$O(n)$
Search	$O(log\ {n})$	$O(log\ n)$
Insert	$O(log\ n)$	$O(log\ n)$
Delete	$O(log\ n)$	$O(log\ n)$

表面上看差不多, 但是细节上,仍然有差别.详情参见Performance Analysis of BSTs in System Software

平衡树这个东西, 除了深度,最基本的, C,R,D, 还有一个重要的考虑点是增,删节点之后的自平衡操作的比较.

深度方向, AVL是比红黑树表现好一点的.但是对于删除来说,AVL最坏情况下,需要$O(log\ n)$}次旋转. 红黑树可以保证稳定的只需要最多2次旋转.算法的可预期程度上来说, 红黑树更稳定,AVL有一点点需要运气.我猜测啊, ConcurrentHashMap作为一个针对缓存做优化的场景,选择红黑树几乎是必须的.

PS

还有一些不知道如何安放的内容.

模10算法来自Hans Peter Luhn. 这位是一个前清时期出生在德意志帝国,工作在IBM的美国计算机科学家,甚至可以算哈希的老祖宗之一
LLRB左倾红黑树, 有的地方会用这个变种
平衡树比较
这次的表格用了markdown 表格生成器
排版换了typora
跳表和平衡树的比较
取自上一个链接的, 无锁版本红黑树文章
ConcurrentSkipListMap图文简介

大多是查了暂时没用上的内容, 或许下一次再写点别的就用上了. 今天说的HashMap,不能并发修改.或许要等到,啥时候真正写 ConcurrentHashMap时候, 会跟ConcurrentSkipListMap一起来做个比较.

为什么Java8在HashMap中使用红黑树?

JEP